题目

若 $ \triangle ABC $ 的外心为 $ O $ ,且 $ \cos A=\dfrac{1}{3} $ ,若 $ \overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC} $ ,则 $ x+y $ 的最大值为
$\qquad A.\dfrac{1}{3}\qquad$ $B.\dfrac{1}{2}\qquad$ $C.\dfrac{2}{3}$ $\qquad D.\dfrac{3}{4}$

解法一

如图，延长 $ AO $ 交 $ BC $ 于点 $ M $ ,设$\overrightarrow{AM}=t \overrightarrow{AO} $ ,则
$$\begin{split}\overrightarrow{AM}=t\overrightarrow{AO}= tx\overrightarrow{AB}+ ty\overrightarrow{AC}\end{split}$$ 因为 $ M,B,C $ 三点共线,所以 $$ tx+ty=1$$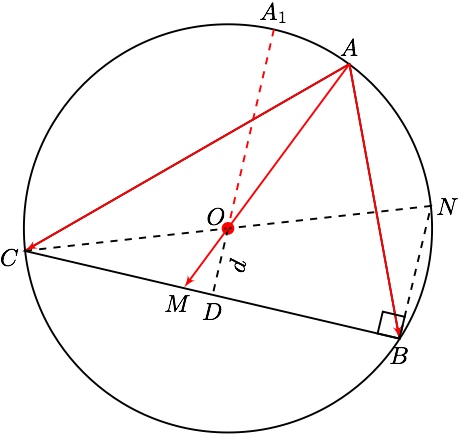

设 $ \odot O $ 的半径为 $ r $ ,点 $ O $ 到直线 $ BC $ 的距离为 $ d $
$$ x+y=\dfrac{1}{t}=\dfrac{|AO|}{|AM|}=\dfrac{r}{r+OM}\leqslant \dfrac{r}{r+d} $$ 当且仅当 $ A=A_1 $ 时，等式成立.
作 $ \odot O $ 的直径 $ CN $ ,连接 $ BN $ ,则
$$ d=\dfrac{1}{2}|BN|=\dfrac{1}{2}\cdot 2r\cos \angle N=r\cos A=\dfrac{r}{3}$$ 所以 $ x+y $ 的最大值为 $ \dfrac{3}{4} $ .

解法二

由 $ \overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC} $ ,统一向量起点为 $ O $ 得
$$ \overrightarrow{AO} = x\left( \overrightarrow{OB}-\overrightarrow{OA} \right)+y\left( \overrightarrow{OC}-\overrightarrow{OA}\right).$$ 整理得 $$ \left( 1-x-y \right)\overrightarrow{OA}+x\overrightarrow{OB}+y\overrightarrow{OC}=\overrightarrow{0}.$$ 1. 若 $ \triangle ABC $ 不为直角三角形,由于 $ O $ 为外心,所以
$$ \dfrac{1-x-y}{\sin 2A}=\dfrac{x}{\sin 2B}=\dfrac{y}{\sin 2C}=\dfrac{1}{\sin 2A+\sin2B+\sin 2C} $$ 所以
$$ x+y=\dfrac{\sin 2B+\sin2C}{\sin2A+\sin2B+\sin2C}=1-\dfrac{\sin 2A}{\sin2A+\sin2B+\sin 2C} $$ 因为
$$ \sin 2B+\sin 2C=2\sin\left( B+C \right)\cos\left( B-C \right)=2\sin A\cos\left( B-C \right)\leqslant 2\sin A $$ 当且仅当 $ B=C $ 等式成立.所以
$$ x+y\geqslant 1-\dfrac{\sin2A}{\sin2A+2\sin A}=1-\dfrac{\cos A}{\cos A+1}=\dfrac{1}{1+\cos A}=\dfrac{3}{4}. $$ 2.若 $ \triangle ABC $ 为直角三角形，则 $ \overrightarrow{AO}=\dfrac{1}{2}\overrightarrow{AB}$ 或 $\overrightarrow{AO}=\dfrac{1}{2}\overrightarrow{AC} $ ,此时 $ x+y=\dfrac 12$.

综上所述， $ x+y $ 的最大值为 $ \dfrac{3}{4} $ .

解法三

以 $ O $ 为原点 $ OA $ 为 $ x $ 轴正方向建立直角坐标系,设 $ A(r,0), B(r\cos\alpha,r\sin\alpha),C(r\cos\beta,r\sin\beta) $ ,